This post will be a conceptual one, rather than technology specific. Imagine a scenario where you want to provide a curated trail experience from a mobile device. You want people to be able to go to a park, pick a starting location (such as their current location) in their device, and query the system for all the possible 1-3 mile loops from that location. How do you rank the looping options, once you’ve calculated what all the possible loops are?

All other things being equal, you might suggest that you want the experience to be as loopy as possible to avoid the Bilbo Baggins problem (There and Back Again):

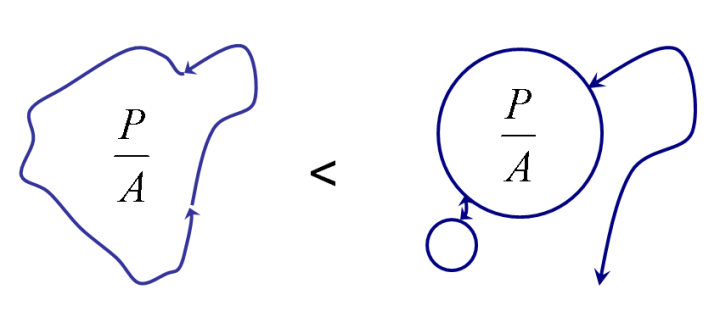
But once you’ve chosen your loopiest trail, the one with the smallest perimeter to area ratio, how do you choose your second best option?  You should choose the next least similar trail loop, so that the user can choose from the maximum diversity of possible choices:

Now we have a clear hierarchy of choices for our trail user, we return the best possible option first, then a list of the options which are least similar.  If you were to offer a 3rd option (three options is a nice place to start to avoid overwhelming the user), that 3rd option should be the second least similar option to the 1st.

The question is, how to do we calculate similarity between routes?  Fuzzy Hashes is the answer.  A fuzzy hash comparison of the pairwise geometries of all the possible loops would give us a matrix of similarity:

Which we can use to complete our trail loop ranking.